模联社 - 强大社员,强大社团 MUN: Strong members make a strong club


模联社:
强大社员,强大社团

MUN: Strong members make
a strong club





上海宏润博源学校模拟联合国队 (SHBS MUN Team) 是一个由学生自主创办的学术竞赛队伍,汇集了来自全校各个年级的优秀学生。模拟联合国队伍成员包括6名各个年级前3,6名全A生,正在迈向一个追求完美,追求精英的学生组织。模拟联合国队旨在“为未来外交官提供展示平台”,秉承“为天地立心,为生民立命”,并不断地自我更新,创造奇迹。

由于模拟联合国活动的特殊性,大部分的训练内容很难在线上展开,创始人蔡晗啸同学和社员们把目光放在了基础知识的学习上。线上学习的2个多月来,他们系统性地学习了“形式逻辑”,有效地提高了各自的批判性思维能力。平时的学习内容由蔡晗啸创作并讲述,梁雨凡、吴文昊两位社团书记进行记录并整理。他们说:“我们整理的形式逻辑讲义尽管不能做到完全系统、专业,但也与此同时可以以通俗的方式让基础薄弱的同学快速入门形式逻辑。在此分享于学校公众号,欢迎对模拟联合国项目有兴趣的同学研读,也借此以飨读者。”


正文

第一讲
1) Father of formal logic: Aristotle
2) Case: William: Sam, who are you talking with?
Sam: I’m talking with nobody
William: Who’s “nobody”?
Analyzation: Here, William played a linguistic game on “names” vs. “quantifiers”
3) Names ≠ quantifiers
4) Some examples for quantifiers: nobody[0人], somebody[若干人], everybody[群体中的一个人]
5) In language, none is none. 在语言中,没有就是没有

第二讲
I. Names vs. Quantifiers
A. “Nobody” is a quantifier that represents the state of non-existence.
B. “Existence” and “non-existence” exist.
C. Q: Is nothing something?
Both nothing and something are quantifiers. However, nothing represents the state of non-existence while something represents the state of existence.
D. Postulate[公理;假设,假定]
Postulates are non-provable beliefs.
Eg1. Postulate: A line is straight.
Eg2. Segment Addition Postulate.
II. Basis of logic
A. Truth value/ validity[有效性](中性词){negative=invalid; positive= valid}
a. Proposition[命题]
Positive = √
Negative= ×
B. Conditionals & their validity
Conditionals(条件句): If…then…
a. The assumption before “then” is a premise[前提条件].
b. The conclusion after “then” is a conclusion.
e.g.: Conditional a. If Leo joins MUN, then, he’ll get smarter.
-validity: negative. Since smart= IQ and IQ of a person cannot be changed.
→ If Leo joins MUN, then, he’ll get more rational.
-validity: positive
b. If Charlotte practices calligraphy every day, then, she’ll improve her skill.
-validity: positive.
Conditional: If…then…
c. 4 types of validity for conditional
i. Positive
ii. Negative
iii. Deductive[推论有效性]
iv. Inductive [归论有效性]
III. Family of conditional
条件句
If… then…
1. Converse: A. If a, then b. / B. If b, then a 逆命题
2. Inverse: if a, then b. / If not a, then not b. not: a negation否命题
3. Contrapositive: If a, then b. / If not b, then not a. 逆否命题
IV. “Or” & “And”
p∩q => p and q “∩”and
p∪q => p or q “∪”or

第三讲
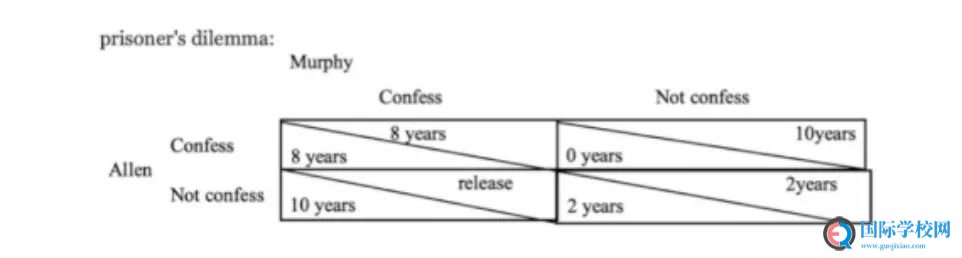
If Murphy has chosen to: Confess Not confess
Then Allen’s best choice: Confess Confess
If Allen has chosen to: Confess Not Confess
Then Murphy’s best choice: Confess Confess

第四讲
Truth table 真值表
Truth table: to represent all the kinds of relationships between two objects.
1
In this picture, s, p have a non-contiguous relation (不接壤关系)
It means whatever s or p is, they have no relationship.

2
In this picture, s, p has a sharing part
It means some part in s and p is same

3
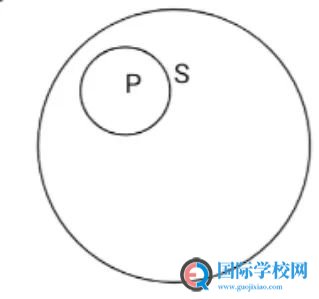
In this picture, s is bigger than p and p is included in s
It means all p is in s but there is still other part in s
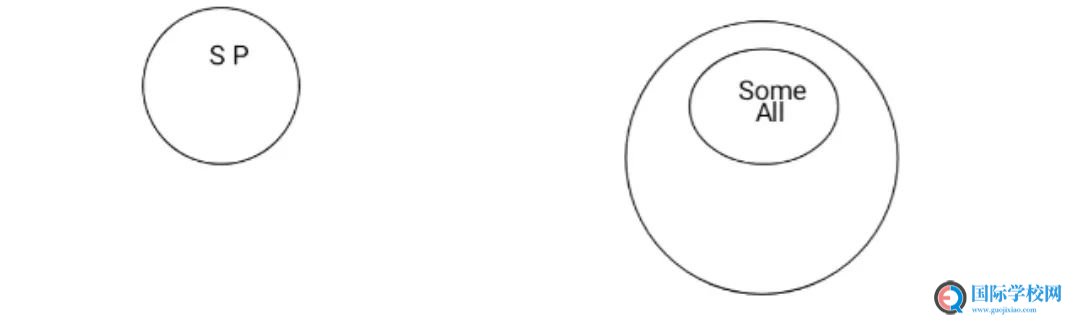
4
In this picture, s is p
It means the description of s is the description of p
Here is the problem which we met in the class
Does “some” equals to “all”?
The answer is yes because “some” is belonged in “all”

第五讲
Name Meaning Notation Example
Negation(负命题) No(并非;不) ¬ ¬P
Conjunction(联言) And(并且;和) ^ p ^ q
Disjunction(选言) Or(或者;要么) ∨ p∨q
Conditional(假言命题) If…then (如果…那么) → p → q
Understand the meaning of every notation and know how to use it

- 上一篇:英国签证|疫情下签证临时调整的详细指引
- 下一篇:害怕绘本里怪兽的孩子
免责声明
(一) 由于各方面情况的调整与变化,本网所提供的【模联社 - 强大社员,强大社团 MUN: Strong members make a strong club】仅供参考,并不意味赞同其观点或证实其内容的真实性,相关信息敬请以权威部门公布的信息为准。
(二) 本网未注明来源或注明来源为其他媒体的稿件均为转载稿,免费转载出于非商业性学习目的,版权归原作者所有,如有内容、版权等问题,请在30日内通过邮件的方式与本网联系。邮箱:myzp@foxmail.com 我们将会在收到邮件后尽快进行处理。
(三) 〖模联社 - 强大社员,强大社团 MUN: Strong members make a strong club〗链接地址:https://guojixiao.com/z/746.html , 转载时请注明来源及保留本站链接。
